吃透高考重难点，拿下高分，椭圆解题策略分析

椭圆这一块知识一直是解析几何的核心内容之一，更是高中数学学习的重点、难点，因此自然成为高考数学命题的热点之一。

椭圆相关的高考题型一般比较新颖，包含各种各样的解题方法,如平面向量与解析几何的融合,提高了题目的综合性,形成了题目多变，解法灵活的特点。

平面内到两个定点F?，F?的距离之和等于常数(大于|F?F?|)的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点F?，F?间的距离叫做椭圆的焦距。

椭圆的定义中应注意常数大于|F?F?|。因为当平面内的动点与定点F?，F?的距离之和等于|F?F?|时，其动点轨迹就是线段F?F?；当平面内的动点与定点F?，F?的距离之和小于|F?F?|时，其轨迹不存在。

椭圆有关的高考试题分析，典型例题1：

在平面直角坐标系中，直线√2x-y+m=0不过原点，且与椭圆y2/4+x2/2=1有两个不同的公共点A，B．

（Ⅰ）求实数m取值所组成的集合M；

（Ⅱ）是否存在定点P使得任意的m∈M，都有直线PA，PB的倾斜角互补．若存在，求出所有定点P的坐标；若不存在，请说明理由．

考点分析：

直线与椭圆的位置关系．

解题反思：

（1）由直线√2x-y+m=0不过原点，知m≠0，将√2x-y+m=0与y2/4+x2/2=1联立，得：4x2+2√2mx+m2-4=0，由此利用根的判别式，能求出实数m的范围组成的集合M．

（2）假设存在定点P（x0，y0）使得任意的m∈M，都有直线PA，PB的倾斜角互补，则kPA+kPB=0，令A（x?，√2x?+m），B（x?，√2x?+m），得：2√2x?x?+（m-√2x0-y0）（x?+x?）2x0（y0-m）=0，由此利用韦达定理能求出所有定点P的坐标．

椭圆有关的高考试题分析，典型例题2：

已知椭圆C?：y2/a2+x2/b2=1（a＞b＞0）的顶点到直线l：y=x的距离分别为√6/2，√2/2．

（1）求椭圆C1的离心率；

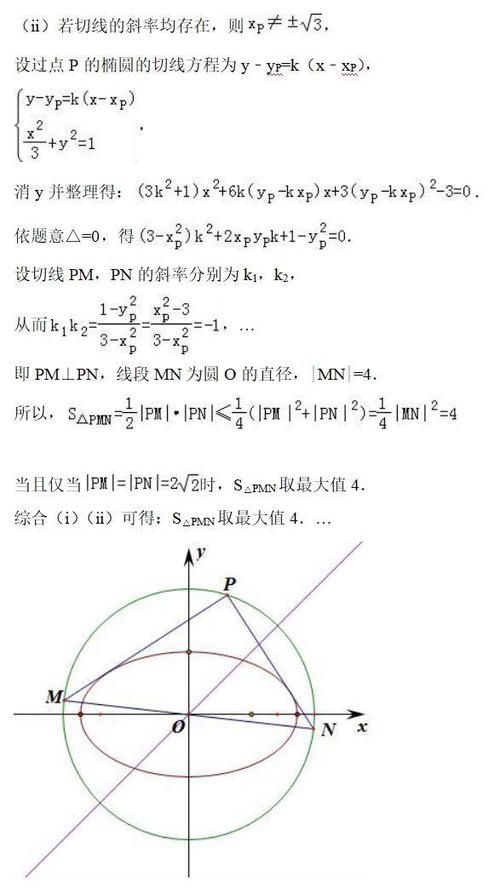
（2）过圆O：x2+y2=4上任意一点P作椭圆C1的两条切线PM和PN分别与圆交于点M，N，求△PMN面积的最大值．

考点分析：

椭圆的简单性质．

题干分析：

（1）根据点到直线的距离公式，即可求得a和b的值，即可求得椭圆的离心率；

（2）分类讨论，当一条切线的斜率不存在时，Xp=±√3，yP=±1，即可求得△PMN面积，当切线的斜率存在时，设切线方程，代入椭圆方程，由△=0，由PM⊥PN，MN|=4.S△PMN=1/2|PM|·|PN|≤1/4（|PM|2+|PN|2）=1/4|MN|2=4，即可求得△PMN面积的最大值．

椭圆有关的高考试题分析，典型例题3：

过椭圆C： x2/2+y2=1的右焦点F的直线l交椭圆于A，B两点，M是AB的中点．

（1）求动点M的轨迹方程；

（2）过点M且与直线l垂直的直线和坐标轴分别交于D，E两点，记△MDF的面积为S1，△ODE的面积为S2，试问：是否存在直线l，使得S1=S2？请说明理由．

考点分析：

直线与椭圆的位置关系；轨迹方程．

题干分析：

（1）：（1）设点M的坐标为（x，y），A（x1，y1）、B（x2，y2）；过椭圆C：x2/2+y2=1的右焦点F（1，0）的直线l为：y=k（x﹣1），联立方程组，消去y，整理得（2k2+1）x2﹣4k2x+2k2﹣1=0，求出动点M 坐标，消去参数k，即可得到 动点M的轨迹方程

（2）假设存在直线AB，使得 S1=S2，确定G，D的坐标，利用△GFD∽△OED，即可得到结论．